You know that it’s necessary to add heat to a substance to increase its temperature, but you might not know that it takes different amounts of heat energy to change the temperature of a specific amount of different substances by 1 degree Celsius. It also takes different amounts of heat energy to increase the temperature of a given amount of a specific substance depending on whether it is a solid, liquid, or gas. Different substances also require different amounts of heat energy to change a given amount of them from solid to liquid or liquid to gas. Showing how we describe these things quantitatively will help to clarify this.

Heat capacity is the quantity of heat that will increase the temperature of a given object by one degree Celsius or one kelvin. (Remember that the magnitude of a degree Celsius is the same as for one kelvin). The object might be a pure compound or element, or it might be a mixture of substances. The most common variable for heat capacity is an uppercase C, and the most common units for it are J/°C, J/K, kJ/°C, or kJ/K. The following formula shows how to calculate the heat necessary to increase an object's temperature by a certain change in temperature (ΔT). We use a lowercase q to represent heat energy.

q = C⋅ΔT

ΔT = T₂ – T₁

For pure elements and compounds, specific heat capacity is more useful. Specific heat capacity (often just called specific heat) is the amount of heat energy (usually in joules) necessary to increase the temperature of one gram of substance by one degree Celsius or one kelvin. The most common variable for specific heat capacity is a lowercase c, and the most common units for it are J⋅g^-1⋅°C^-1 or J⋅g^-1⋅K^-1. The following equation allows us to calculate the amount of heat energy necessary to increase the temperature of a given mass (m) of substance by a certain amount (ΔT):

q = m⋅c⋅ΔT

The following is a table of some common specific heat capacities at constant pressure and 25 °C, unless otherwise noted.

Note that there is a significant variation in specific heat capacities, and note that the same substance (in this case water) has different specific heat capacities depending on whether it is a solid, liquid, or gas. Also, note that liquid water has an especially high specific heat capacity.

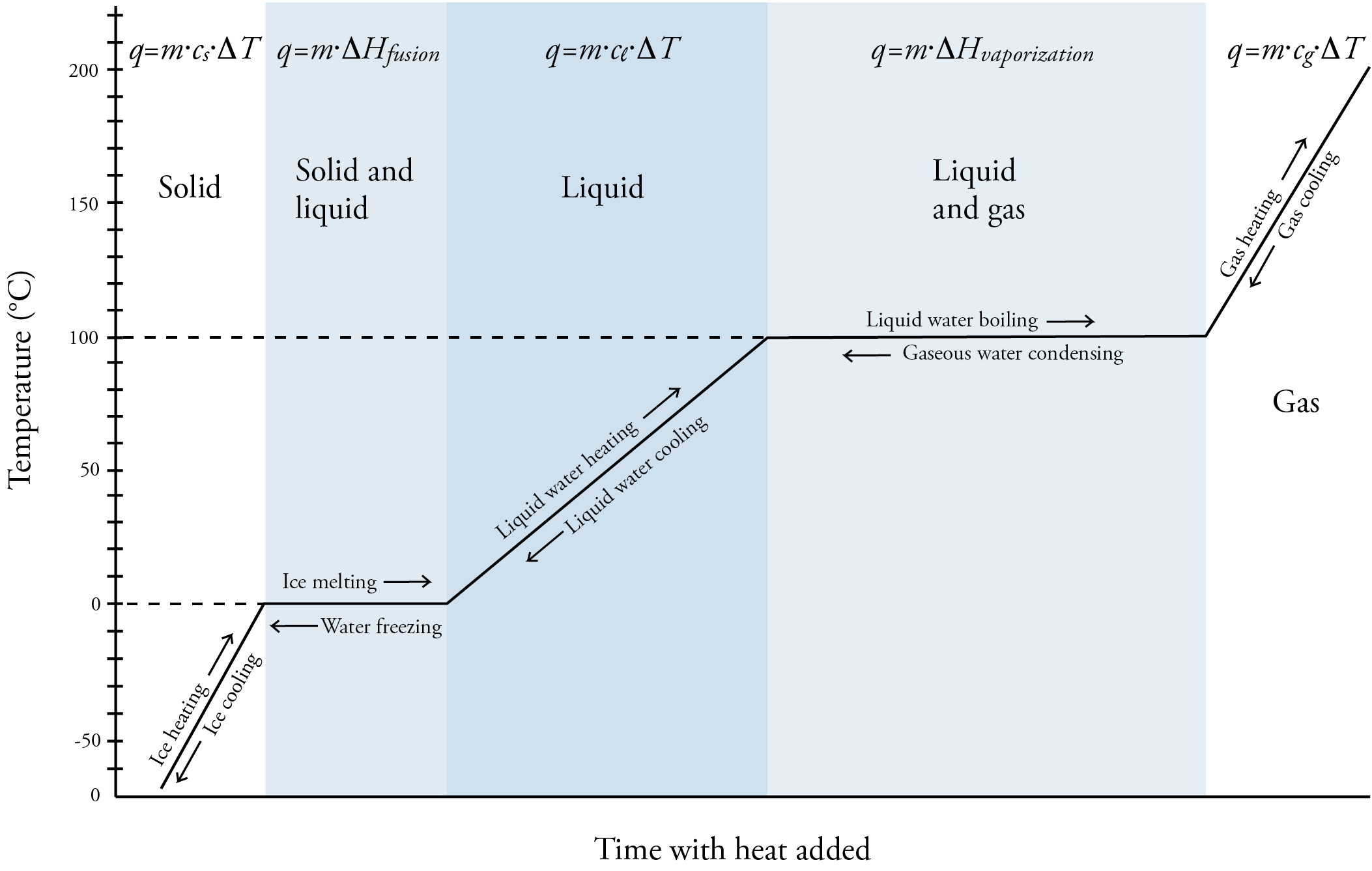
Now let’s consider the energy associated with the phase changes of solid to liquid (melting). Heat of fusion, ΔH_fus, is the heat energy necessary to convert a given amount of solid to liquid at constant pressure. (In this context, fusion is another word for melting.) The units for ΔH_fus vary, but it is commonly described in J/g. Like specific heat capacities, heats of fusion vary from one substance to another. For example, it is 333.55 J/g for water, 97.99 J/g for acetone, and 58.99 J/g for methane. Note that water has a relatively high heat of fusion compared to the others. The following equation can be used to calculate heat energy associated with the melting process.

q = m⋅ΔH_fus

The conversion of liquid to solid (solidification) is just the opposite of solid to liquid (fusion), so the heat of solidification, ΔH_{solidification}, is just the opposite of the heat of fusion. For example, the heat of solidification of water is -333.55 J/g. (The ΔH for energy absorbed, such as for the melting process, is described as positive, and the ΔH for energy released, such as for the solidification process, is described as negative.)

Next, let’s consider the energy associated with the phase changes of liquid to gas (boiling or vaporization). Heat of vaporization, ΔH_vap, is the heat energy necessary to convert a given amount of liquid to gas at constant pressure. Like for ΔH_fus, ΔHvap is commonly described in J/g. Like for heats of fusion, heats of vaporization vary from one substance to another. For example, it is 2257 J/g for water, 538.9 J/g for acetone, and 480.6 J/g for methane. Note that water has a relatively high heat of vaporization compared to the others and that heats of vaporization are significantly higher than heats of fusion for each substance. The following equation can be used to calculate heat energy associated with the vaporization process.

q = m⋅ΔH_vap

The conversion of gas to liquid (condensation) is just the opposite of liquid to gas (vaporization), so the heat of condensation, ΔH_condensation, is just the opposite of the heat of vaporization. For example, the heat of condensation of water is -2257 J/g.

Now let’s consider the changes that a substance, such as water, undergoes as heat is added constantly to a solid form of the substance. See the image below. At first, adding heat increases the temperature of the solid. We could do calculations for this stage using the specific heat equation that includes the specific heat capacity of the solid (c_s).

q = m⋅c_s⋅ΔT

When the temperature reaches the melting point temperature of the substance (0 °C for water), the substance begins to melt. While the solid is still changing to a liquid, the temperature stays constant because the energy added is converted into potential energy not kinetic energy. The melting process disrupts some of the attractions between the particles, and the weaker attractions between the particles in the liquid make the liquid less stable and higher potential energy than the solid. Temperature is a measure of the average internal kinetic energy of a substance, so if the kinetic energy is not increasing, neither is the temperature. Calculations relating to the melting process can be done with the following equation.

q = m⋅ΔH_fus

When all the solid has been converted into liquid, the energy added goes to increasing the kinetic energy and therefore the temperature of the substance. We could do calculations for this stage using the specific heat equation that includes the specific heat capacity of the liquid (c_l).

q = m⋅c_l⋅ΔT

When the temperature reaches the boiling point temperature of the substance (100 °C for water), the substance begins to boil and liquid is converted to gas. While the liquid is still changing to a gas, the temperature stays constant because, once again, the energy added is converted into potential energy not kinetic energy. Calculations relating to the vaporization process can be done with the following equation.

q = m⋅ΔH_vap

When all the liquid has been converted into gas, the energy added goes to increasing the kinetic energy and therefore the temperature of the substance. We could do calculations for this stage using the specific heat equation that includes the specific heat capacity of the gas(c_g).

q = m⋅c_g⋅ΔT

The image below shows the changes from solid to liquid to gas and gas to liquid to solid.